Erone

Un altro sostenitore della teoria dell'emissione fu Erone Alessandrino. Il suo lavoro per noi assume un rilievo particolare: Erone infatti è il primo a utilizzare in maniera scientificamente valida un principio regolativo di grande portata euristica nello sviluppo della scienza, il principio variazionale della minima distanza, mediante il quale deduce correttamente le leggi della riflessione (Erone evidentemente non riesce a dimostrare sulla base dello stesso principio la legge della rifrazione poiché in questo caso il punto di incidenza non minimizza il percorso ottico tra l'occhio e l'oggetto). Vale la pena tuttavia sottolineare nel caso in esame l'interessante connessione tra ottica geometrica, ottica fisica (nucleo di assunzioni base) e idee regolative (tematiche di fondo) e il ruolo non trascurabile svolto da queste ultime nella spiegazione di un fenomeno fisico. I principi di minimo sono stati spesso collegati a concezioni antropomorfiche sul comportamento della natura («la luce sceglie il suo percorso») e quindi guardati con sospetto. Essi possono invece essere considerati come espressione scientifica delle categorie teleologiche, di pari utilità e dignità di quelle causali. Nel corso della nostra analisi vedremo che hanno svolto un ruolo notevole nello sviluppo dell'ottica.

Erone, Catottrica , II, pp. 263-64

L'affermazione che la nostra vista procede in linea retta provenendo dall'occhio può essere fondata come segue. Ciò che si muove con velocità costante si muove in linea retta. Le frecce tirate da un arco possono servire da esempio. Ciò avviene poiché la forza impressa costringe l'oggetto a muoversi per la distanza più breve possibile dal momento che non ha il tempo per un moto più lento, cioè per un moto su un percorso maggiore. La forza impressa non permette un tale ritardo e così, a causa della sua velocità, l'oggetto tende a muoversi sulla traiettoria più breve. Ma la più breve delle linee avente gli stessi punti estremi è la linea retta.

Che i raggi provenienti dai nostri occhi si muovono con velocità infinita può essere compreso dalla considerazione seguente: quando, dopo aver chiuso gli occhi li apriamo e guardiamo il cielo, il raggio visuale non ha bisogno di tempo per raggiungere il cielo. Infatti vediamo le stelle nello stesso istante in cui le guardiamo sebbene la distanza sia, per così dire, infinita. E anche se questa distanza fosse maggiore il risultato sarebbe lo stesso, pertanto è chiaro che i raggi sono emessi con velocità infinita. Per conseguenza essi non subiscono interruzione, incurvamento o deviazione ma si muoveranno lungo il percorso più breve, la linea retta.

Abbiamo mostrato a sufficienza che la nostra vista procede in linea retta. Ora mostreremo che i raggi incidenti sugli specchi e anche sull'acqua e sulle superfici piane sono riflessi [.... In base a considerazioni sulla velocità di incidenza e di riflessione, dimostreremo che questi raggi sono riflessi ad angoli uguali nel caso degli specchi piani e sferici.

Per la nostra dimostrazione faremo ancora uso di linee di minimo. Dico allora che di tutti i raggi incidenti, riflessi in un punto dato da uno specchio piano o sferico, i più brevi sono quelli che sono riflessi ad angoli uguali e, se accade ciò, la riflessione ad angoli uguali è conforme a ragione.

AB sia uno specchio piano, G l'occhio, D l'oggetto da osservare (cfr. fig. 1) e AG sia un raggio incidente sullo specchio. Tracciamo AD e poniamo EAG = BAD. GB sia un altro raggio incidente sullo specchio. Tracciamo BD. Affermo che: GA + AD < GB + BD.

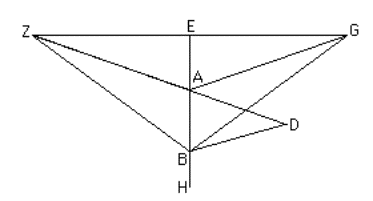
Fig. 1

Abbassiamo da G la perpendicolare ad AB, GE; prolunghiamo poi GE e AD fino a che essi si incontrano in Z. Tracciamo ZB. Ora BAD = EAG, inoltre BAD = ZAE perché angoli al vertice, perciò ZAE = EAG.

Dato che gli angoli in E sono retti ZA = AG e ZB = BG. Ma ZD < ZB + BD e ZA = AG, ZB = BG perciò GA + AD < GB + BD. Ora EAG = BAD e EBG < EAG, HBD > BAD. Perciò a fortiori sarà HBD > EBG.