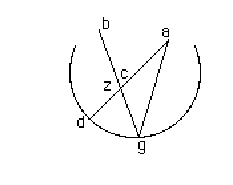Euclide
Con Euclide l'ottica viene per la prima volta strutturata in assiomi e teoremi: nella sua opera, Ottica e Catottrica, sono contenuti elementi di prospettiva, lo studio della riflessione negli specchi piani e sferici e, per la prima volta, viene definito il concetto di raggio visuale come privo di struttura fisica. Ciò permette a Euclide di estendere il metodo tipico delle dimostrazioni geometriche al campo dei fenomeni luminosi. All'Ottica e alla Catottrica viene premesso un certo numero di «supposizioni» dalle quali vengono derivati i teoremi. Tali assiomi in realtà non hanno quel carattere di rigore logico proprio degli assiomi degli Elementi ma piuttosto sono il risultato di un compromesso tra dati assunti sperimentalmente e dati nei quali elementi spaziali e geometrici si intrecciano a considerazioni di carattere soggettivo.
Il primo postulato dell'Ottica, relativo alla propagazione rettilinea dei raggi visuali emessi dall'occhio, costituisce il fondamento dell'ottica geometrica euclidea. Esso infatti pone sia il concetto di raggío come modo di propagazione della luce, come filetto elementare di luce, sia il concetto di propagazione rettilinea. Teone Alessandrino (IV secolo d. C.) il curatore della riedizione dei libri di Euclide, riporta alcune tracce delle argomentazioni che condussero Euclide ai suoi postulati: per il primo c'è il richiamo a esperienze condotte con fessure fatte su tavolette di legno allineate con una fiamma. Il secondo postulato dell'Ottica sarà importante per i successivi sviluppi dell'ottica fisiologica: «la figura compresa dai raggi visuali è un cono che ha il vertice nell'occhio e la base al margine dell'oggetto». La concezione emissionista trova esplicita menzione nella terza e quarta supposizione. Gli unici oggetti che si possono vedere sono quelli sui quali arrivano i raggi visuali, cioè i raggi emessi dall occhio.
Di particolare interesse i primi due assiomi della Catottrica, il primo dei quali attribuisce al raggio visuale la proprietà di essere rettilineo nel caso in cui «il punto medio del raggio copre gli estremi», mentre il secondo ribadisce che ogni cosa visibile si vede per linea retta. Il primo assioma sembra essere stato enunciato allo scopo di preparare la via ai teoremi (Catottrica, teoremi XVI, XVII, XVIII) nei quali si determina la posizione dell'immagine di un oggetto formata dagli specchi piani e sferici, mentre il secondo potrebbe avere lo scopo di «salvare» l'edificio dell'ottica, interamente basato sulla propagazione rettilinea dei raggi visuali. Sta di fatto però che già nel caso della riflessione (proprio il caso esaminato nella Catottrica), il raggio visuale viene deviato dal suo cammino rettilineo ed Euclide sembra allora adombrare una differenza di comportamento tra raggio visuale e raggio di luce riaffermando solo per il primo — e per il suo prolungamento — la proprietà di procedere sempre in linea retta. Restano tuttavia non poche perplessità sul comportamento e sulla natura del raggio visuale nel caso di deviazione dalla linea retta.
Si noti infine che nella trattazione degli specchi sferici (Catottrica, teoremi XVII, XVIII) Euclide, e con lui Tolomeo, localizza l'immagine nel punto di intersezione tra la linea congiungente il punto oggetto con il centro di curvatura dello specchio e il prolungamento della linea che va dall'occhio alla superficie riflettente. Ciò in realtà è valido solo nel caso in cui l'angolo acuto formato dalle due linee è assai piccolo. Il terzo postulato della Catottrica conduce direttamente a uno dei più famosi teoremi, quello esprimente le leggi di riflessione (Catottrica, teorema I). Confronteremo nel seguito questo tipo di dimostrazione con quella di Erone Alessandrino basata sui principi variazionali. Mentre Euclide postula la propagazione rettilinea della luce, Erone tenterà di dimostrarla mediante argomentazioni di carattere teleologico (principi variazionali di minimo) assunte come idee regolatrici. Tolomeo, e più tardi Alhazen e Witelo, ne daranno invece dimostrazione sperimentale.
Per concludere questa rapida analisi dell'ottica
euclidea possiamo affermare che essa si presenta come una sintesi ben
strutturata in assiomi e teoremi delle principali conoscenze di ottica
dell'antichità. La natura di tali assiomi tuttavia risulta fortemente
condizionata dall'idea che la visione avvenga per raggi emessi dall'occhio.
Questa assunzione rende assai complesso il problema di descrivere
geometricamente una realtà che, pur essendo esterna all'osservatore, continua a
essergli legata da quei «prolungamenti fisiologici» che sono i raggi visuali.
D'altro lato, la definizione di raggio come ente matematico insieme all'idea
che dall'occhio possa essere emesso un cono di raggi, con vertice nell'occhio
stesso, considerato puntiforme, e base sull'oggetto, costituiscono di fatto una
innovazione metodologica di gran rilievo che rende possibile l'estensione del mos geometricus all'ottica. Euclide
accenna appena alla rifrazione, alla quale Tolomeo dedicherà invece ampio
spazio.
Euclide,
Prospettiva, pp. 80-84
Supposizione I
Presuppongasi adunque che i raggi ch'escano dall'occhio,
sieno portati per retta linea, e che con qualche intervallo sieno l'uno
dall'altro lontani.
Supposizione II
La figura compresa da' raggi visuali è un Cono la cui punta
è nell'occhio e la basa è nell'estremità della cosa veduta.
Supposizione III
Quelle cose si veggono, alle quali arrivono i raggi
visuali.
Supposizione IV
Quelle cose non si possono vedere, alle quali non arrivono
i raggi visuali.
Supposizione V
Quelle cose che sotto maggiore angolo si veggono, ci
appariscono maggiori.
Supposizione VI
Quelle cose che sotto minori angoli si veggono ci
appariscono minori.
Supposizione VII
Quelle cose che sotto eguale angolo si veggono ci
appariscono eguali.
Supposizione VIII
Quelle cose, che da più alti raggi sono viste, più alte ci
appariscono.
Supposizione IX
Quelle cose che da' raggi più bassi sono viste, più basse
ci appariscono.
Supposizione X
Quelle cose che sono viste da' raggi che più piegano dalla mano
destra, ci appariscono più destri.
Supposizione XI
Quelle cose, che sono viste da' raggi che più piegano alla
sinistra, ci appariscono più sinistri.
Supposizione XII
Quelle cose che si vedono sotto più angoli, si vedono più
distintamente.
Euclide,
Prospettiva, pp. 95-107
Supposizione I
Presuppongasi che il raggio visuale sia una linea retta,
della quale i mezzi cuoprono gli stremi.
Supposizione II
Ogni cosa visibile si vede per retta linea.
Supposizione III
Se lo specchio si collocherà in un piano, sopra il quale
stia a piombo qualche altezza, la ragione, che harà la linea intrapresa fra
quel che mira et lo specchio, alla linea che è fra lo specchio et la già detta
altezza, harà anco l'altezza di quel che mira all'altezza della cosa elevata a
piombo, sopra il piano nel quale è lo specchio. [1]
[1] Se ca rappresenta lo specchio, gz il piano, bg l'altezza
perpendicolare a esso, dz l'altezza dell'osservatore, si avrà cioè, zt: tg =
dz: gb. Questa supposizione viene introdotta per dimostrare il teorema I.
 Supposizione
IV. Apparenza I [2]
Supposizione
IV. Apparenza I [2]
Se l'occhio si porrà in quel punto dello specchio piano ove
percuote a piombo la linea, che viene dalla cosa visibile, detta cosa non si
potrà vedere.
[2] I quattro assiomi che seguono vengono definiti apparenze
poiché si riferiscono a ciò che si suppone
apparire agli occhi nostri e non a ciò che realmente è.
Supposizione V. Apparenza II
Negli specchi rotondi, se l'occhio si porrà in quel luogo
ove passa la linea, che partendosi dalla cosa visibile, va al centro dello
specchio, detta cosa non si potrà vedere.
Supposizione VI. Apparenza III
Il medesimo avviene negli specchi concavi, che avveniva ne'
convessi, o rotondi che dir vogliamo.
Supposizione VII. Apparenza IV
Se si porrà a qual si voglia cosa, nel fondo d'un vaso, poi
si discosti tanto dall'occhio, che la cosa già detta non si vedi più, dico che
tal cosa si potrà vedere in questo luogo, se il vaso si empierà d'acqua.
[. ]
Il Fine delle
suppositioni
THEOREMA PRIMO
I raggi visuali si
rilfettono ad angoli pari, tanto negli specchi piani, come anco ne' rotondi, et
ne' concavi.
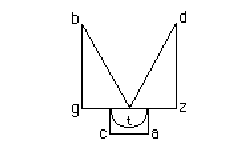
Sia l'occhio nel punto b & lo specchio piano sia ag
& esca dall'occhio il raggio bc che si rifletta nel punto d. Dico che
l'angolo della reflessione e è eguale all'angolo della incidenzia z. Imperoche,
tirinsi le due linee a piombo bg & da sopra lo specchio ag. Et sarà la bg
alla gc come è la da alla ac (per la terza suppositione) per il che il
triangolo bgc sarà simile al triangolo dac tal che l'angolo e sarà eguale
all'angolo z essendo i triangoli simili di angoli eguali.
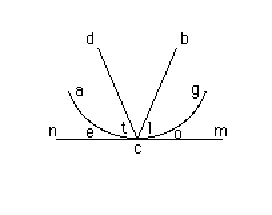
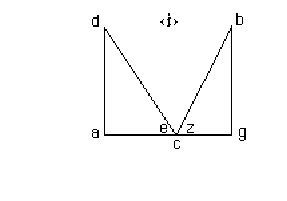 Dimostratione nello specchio rotondo
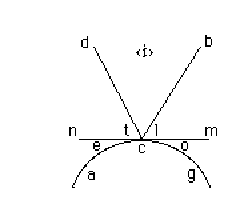
Dimostratione nello specchio rotondo
Sia lo specchio rotondo la acg & il raggio visuale sia
bc che si rifletta nel punto d. Dico che l'angolo dell'incidentia ol è eguale
all'angolo della reflessione et perche se io porrò uno specchio piano nella
linea nm di maniera, che tocchi lo specchio tondo nel punto c l'angolo t sarà
eguale all'angolo l. Ma l'angolo e è eguale all'angolo o perche lo specchio nm
piano tocca lo specchio acg rotondo; onde tutto l'angolo te sarà eguale a tutto
l'angolo lo.
 Dimostratione
nello specchio concavo
Dimostratione
nello specchio concavo
Sia lo specchio concavo acg & il raggio visuale sia bc
che si rifletta nel punto d. Dico, che l'angolo t è eguale all'angolo 1.
Impercioche, ponendovi lo specchio piano mn sarà eguale l'angolo te all'angolo
lo. Ma l'angolo e è eguale all'angolo o. Onde il rimanente angolo t sarà eguale
al rimanente angolo l.
 THEOREMA SECONDO
THEOREMA SECONDO
Se il raggio
visuale cascando sopra qual si voglia specchio, nel punto della incidentia farà
angoli puri, si rifletterà in se stesso.
Sia la acg lo specchio stia nel piano, & l'occhio stia
nel punto b dal quale esca il raggio be che faccia sopra lo specchio angoli
eguali, cioè l'angolo ze eguale all'angolo l. Dico che riflettendosi il raggio
bc si riflettera, & ritornera in se stesso, cioè nel b punto dell'occhio.
Il che non essendo così riflettisi se è possibile nel punto d. Hor perche i
raggi si riflettono ad angoli eguali, l'angolo z sarà eguale all'angolo l ma già
si è detto che l'angolo ze è eguale all'angolo l; adunque l'angolo ze sarà
eguale all'angolo z il maggiore al minore, il che è impossibile. Adunque il
raggio bc si riflette in se stesso. Questa medesima dimostratione si puote
accomodare ancora a gli specchi rotondi, & concavi.
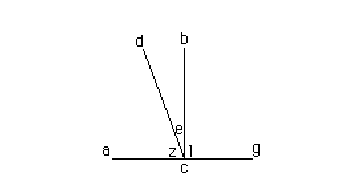 THEOREMA TERZO
THEOREMA TERZO
Il raggio visuale,
cascando sopra qual si voglia specchio, et facendo angoli ineguali, non si
riflette in se stesso, ne manco verso il minore angolo.
Sia lo specchio piano la acg & il raggio bc
percuotendovi sopra, faccia l'angolo z maggiore dell'angolo lt. Dico che
riflettendosi il raggio bc non si riflette in se stesso ne manco diverso
l'angolo lt. Perche riflettendosi in se stesso cioè nella bc l'angolo z sarà
eguale all'angolo lt il che è falso, perche l'angolo z si è posto maggiore
dell'angolo lt. Ma se si rifletterà nel punto d l'angolo z sarà eguale
all'angolo lche gia si è posto maggiore. Per il che il raggio bc si rifletterà
verso l'angolo maggiore, che è nella z awenga, che dall'angolo maggiore, si
potra tagliare un angolo eguale al minore. Nel medesimo modo si può dimostrare
negli specchi rotondi, & concavi. [...]
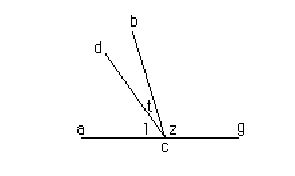 THEOREMA SESTODECIMO
THEOREMA SESTODECIMO
Ciascuna cosa visibile negli specchi piani, si vede nella
linea perpendicolare, tirata dalla cosa visibile, fino allo specchio.
Sia lo specchio piano gd & l'occhio sia il punto b
& la cosa visibile il punto a & dalla a cosa visibile si tiri fino allo
specchio la perpendicolare ag. Hor perche nella prima apparenza si è posto,
& concesso, che il punto a non si possa vedere dall'occhio posto nel punto
g seguirà che il punto a si vegghi in qualche punto della linea ag tirata,
& distesa in lungo, si vedrà anco da qualche punto del raggio visuale bd
tirato, & disteso flno al punto e dal qual punto si vedrà la cosa visibile
a. Et perche si è posto nella prima suppositione di questo libro, che quel
raggio è retto, del quale i mezzi cuoprono gli estremi, i raggi ae & be
saranno retti.
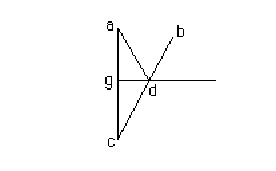 THEOREMA DECIMOSETTIMO
THEOREMA DECIMOSETTIMO
Negli specchi rotondi qual si voglia cosa visibile si vede
nella linea retta, che dalla cosa visibile va al centro dello specchio.
Sia lo specchio rotondo dg & l'occhio sia il punto b e
'l raggio, che esce dall'occhio bd il quale si rifletta nel punto a che è la
cosa visibile, & la z sia il centro dello specchio, del quale è parte gd
& congiungasi la retta linea az stendendo il raggio visuale bd fino al
punto e. Hor perche nella seconda apparenza si è posto che la a non si può
vedere dall'occhio, che sta nel punto g adunque la cosa visibile a sarà vista
in qualche punto della linea ag tirata, & distesa in lungo, cioè in quel
punto ove il raggio bd disteso, & allungato rettamente, si congiugne con la
linea ag che sarà (come negli specchi piani) il punto e.
 THEOREMA DECIM OTTAVO
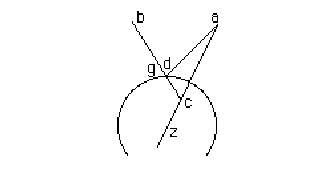
THEOREMA DECIM OTTAVO
Negli specchi
concavi, qual si voglia cosa visibile si vede nella linea retta, che dalla cosa
visibile va al centro dello specchio.
Sia lo specchio concavo gd e 'l raggio visuale che esce
dall'occhio bg che si rifletta alla cosa visibile a & il centro dello
specchio concavo sia il punto c del quale è parte lo specchio gd &
congiunghisi la linea ae stendendola à dirittura, hor perche nella terza
apparenza si è posto, che il punto a non si può veder dall'occhio che stà nel
punto d adunque l'imagine della cosa visibile a si vedrà in qualche punto della
linea ae distesa, & allungata à dirittura il qual sarà il punto z ove la
linea ad concorre, & si taglia col raggio bg.