Fermat
Dopo la pubblicazione della Dioptrique, lo stesso Fermat (1601-65) in più riprese aveva accusato Cartesio di aver usato nella sua dimostrazione ipotesi ad hoc. La decomposizione del moto della luce, secondo Fermat, era arbitraria e inoltre mal si conciliava con l'ipotesi postulata da Cartesio che la luce dovesse propagarsi istantaneamente; l'affermazione che la velocità della luce dovesse essere maggiore in acqua che in aria, inoltre, era inammissibile e andava contro ogni buon senso. Lo stesso Fermat deriverà nel 1662 la legge della rifrazione in base al principio di minimo secondo il quale il tempo che la luce impiega per propagarsi in due o più mezzi ottici deve essere minimo; egli trova la legge, che oggi sappiarno essere corretta, sen i/sen r = vi/vr Le idee di Fermat, accusato dagli stessi cartesiani di condurre dimostrazioni non causali bensì teleologiche, tuttavia non troveranno accoglienza negli ambienti accademici e l'ffermazione che la velocità della luce debba aumentare nei mezzi più densi dominerà le ricerche di ottica per oltre due secoli.
P. Fermat, OEuvres , III, p. 156
Sia
ACBI un cerchio il cui diametro AFDB separi due mezzi di natura diversa, il
mezzo meno denso stando dalla parte ACB e quello più denso dalla parte AIB
(cfr. fig. 1).
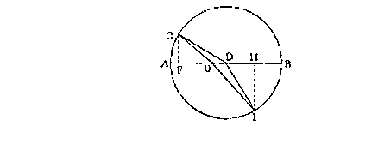
Sia D il centro del cerchio e CD un raggio incidente che
cade su questo centro da un dato punto C; si richiede di trovare il raggio
rifratto DI, o altrimenti il punto I attraverso il quale il raggio passa dopo
la rifrazione.
Facciamo
cadere le perpendicolari CF, IH sul diametro. Poiché il punto C è dato, così
come pure il diametro AB ed il centro D, il punto F e la linea FB sono anche
date. Supponiamo che il rapporto della resistenza del mezzo più denso rispetto
a quella del mezzo meno denso sia uguale al rapporto della linea retta data DF
ad un'altra linea m disegnata fuori della figura. Dovremmo avere m <DF,
poiché la resistenza del mezzo meno denso dovrebbe essere minore di quella del
mezzo più denso, per un assioma che è naturale adottare.
Dobbiamo
adesso misurare per mezzo delle linee m e DF, i moti lungo le linee CD e DI;
possiamo dunque rappresentare proporzionalmente l'intero moto lungo queste due
linee per mezzo della somma dei due prodotti: DC m + DI DF.
Il
problema si riduce pertanto a quello di dividere il diametro AB nel punto H in
modo tale che se in questo punto tiriamo una perpendicolare HI e poi uniamo DI,
l'area CD m + DI DF deve essere un minimo.
Per
compiere ciò dobbiamo impiegare il nostro metodo che è già diffuso tra i
matematici e fu presentato circa 20 anni fa da Herigone nel suo Cursus Mathematicus. Usiamo n per
rappresentare il raggio CD o il suo equivalente DI, b per rappresentare la
linea DF e poniamo DH = a. La quantità nm + nb dovrebbe essere un minimo.
Per
l'incognita e prendiamo una linea arbitraria DO; uniamo CO con OI. In notazione
analitica abbiamo CO2 = n2 + e2 _ 2be e OI2 = n2 + e2 + 2ae; allora
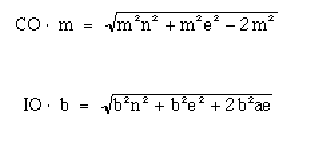
La
somma di questi due radicali dovrebbe essere posta uguale, in accordo alle
regole dell'arte, alla somma mn + bn.
Per
eliminare i radicali, eleviamo al quadrato entrambi i membri dell'equazione,
cancelliamo i termini comuni, e trasponiamo in modo che su un lato
dell'equazione sia lasciato solo il radicale che rimane; poi eleviamo al
quadrato di nuovo entrambi i membri; dopo un'altra cancellazione di termini
comuni su entrambi i membri, dividendo tutti i termini per e ed eliminando
tutti quelli in cui ancora rimane, in accordo alle regole del nostro metodo,
che è già generalmente noto da un certo tempo, raggiungeremo infine,
cancellando i fattori comuni, la più semplice equazione possibile tra a e m,
cioè a dire, quando ci saremo sbarazzati delle difficoltà date dai radicali,
troveremo che la linea DH della figura è uguale alla linea m.
Ne
segue che per cercare il punto di rifrazione dobbiamo, quando abbiamo tirato le
linee CD e CF, prendere le linee DF e DH nel rapporto della resistenza del
mezzo più denso a quella del mezzo meno denso, oppure nel rapporto di b a m.
Alziamo allora in H la linea HI perpendicolare al diametro; essa taglierà il
cerchio in I, punto per il quale passerà il raggio rifratto; così procedendo,
il raggio, passando da un mezzo meno denso ad uno più denso, sarà deviato verso
la perpendicolare.
Questo risultato è in perfetto accordo e senza eccezione al teorema scoperto da Descartes: la precedente analisi basata sul nostro principio dà pertanto a questo teorema una dimostrazione che è rigorosamente esatta.
P. Fermat, OEuvres, II , pp. 485-89
Signore
dato
che il Sig. di XXX ne parla e lo richiedete voi Signore, la cui reputazione è
cosl alta e ben conosciuta, risveglierò la mia Geometria che ha sonnecchiato
per così lungo tempo e senza altro indugio vorrei raccontarvi la storia della
nostra Dioptrique e della nostra rifrazione; la narrerò come
una favola lasciando così il vostro giudizio libero in modo che possiate
esprimere iI vostro punto di vista senza preoccupazione. Dopo aver visto il
libro del defunto Sig. Descartes e dopo aver attentamente esaminato la
proposizione che è alla base della sua Dioptrique e che stabilisce il rapporto [ratio] di
rifrazione, divenni sospettoso sulla sua prova dato che la sua dimostrazione mi
appariva come un vero paralogismo. Dapprima perché egli la basa su un paragone
e lei sa che la Geometria non dà molto peso a questo metodo dato che i paragoni
in questi casi sono spesso anche più odiosi di quelli ordinari; poiché egli
suppone poi che il moto della luce in aria e nei corpi rarefatti è più
difficile, o se voi preferite, più lento del moto nell'acqua e negli altri
corpi densi, il che mi sembra offenda il senso comune; infine poiché egli
afferma che una delle direzioni o delle determinazioni del moto di una palla
sussiste interamente dopo aver incontrato il secondo mezzo; io aggiunsi anche
altre ragioni che sarebbe stancante o superfluo raccontare. Egli vide i miei
scritti, ad essi rispose e dopo una lunga corrispondenza e molte discussioni ci
separammo come l'accusato ed il testimone, l'uno asserendo e l'altro negando i
fatti, sebbene alla fine io abbia ricevuto da lui delle lettere molto gentili.
Dopo la sua morte, avendo il Sig. de la Chambre pubblicato
il suo trattato sulla luce ed avendomi onorato dell'omaggio di una copia, colsi
l'opportunità di scrivergli la lettera che avete letto, nella quale suggerivo
che l' unico modo per evitare paralogismi in un soggetto così oscuro, era di
cercare la spiegazione della rifrazione in quest'unico principio, cioè che la
natura agisce sempre per la via più breve. Su questa base io suggerii che si
poteva cercare per via geometrica il punto di rifrazione riducendolo al
problema o teorema che voi conoscete. Dato che, comunque, io reputavo che
questo metodo fosse molto difficile e complesso, poiché queste questioni di
massimi e minimi generalmente portano a operazioni molto intricate che possono
essere facilmente confuse per l'illimitata asimmetria che si incontra nel
lavoro, io fermai i miei pensieri a questo stadio e per molti anni ho aspettato
che qualche geometra, meno pigro di me, facesse o la scoperta o la
dimostrazione. Ma nessuno ebbe voglia di intraprendere questo lavoro. Nel
frattempo, di tanto in tanto, ricevetti lettere dal Sig. de la Chambre nelle
quali mi spingeva ad aggiungere la Geometria al mio Principio e a metter giù
una dimostrazione che potesse servire come reale fondamento alla rifrazione.
Ciò che mi tratteneva, inoltre, era l'assicurazione data dal Sig. Petit e da
altri, che i loro ripetuti esperimenti per misurare la rifrazione in acqua, nel
cristallo, nel vetro e in molti altri liquidi, erano in perfetto accordo con la
proposizione del Sig. Descartes, cosicché mi sembrò inutile tentare di trovarne
un'altra per mezzo del mio principio, dato che la natura sembrava pronunciarsi
così decisamente a suo favore.
L'obiezione
che voi sollevate nella vostra lettera non mi impensierì realmente per il
fatto, che avevo già espresso nella mia lettera al Sig. de la Chambre, che ogni
cosa che tocca o si ferma in un punto di una curva è come se toccasse o si
fermasse in un punto della tangente alla curva in quel punto particolare,
cosicché sebbene la somma di due linee di riflessione può essere qualche volta
massima in specchi concavi, sferici o di qualunque altra forma, essa è sempre
la più piccola di tutte quelle che possono cadere sulla linea o sul piano che
tocca gli specchi nel punto di riflessione e ciò non richiede ulteriori prove
dato che il Sig. Descartes lo assume così come faccio io.
Tutte le difficoltà erano pertanto ridotte al fatto che
sembrava che io dovessi combattere non solo gli uomini ma anche la natura. Comunque,
le ultime insistenze del Sig. de la Chambre furono così intense che due o tre
anni fa decisi di cercare l'aiuto della mia analisi credendo che ci fosse
un'infinità di proposizioni differenti l'un l'altra e la cui diversità il senso
non poteva verificare cosicché poteva accadermi di trovarne una che poteva
essere molto vicina a quella del Sig. Descartes senza essere la stessa. Ho
portato avanti la mia analisi per mezzo di un mio proprio metodo particolare e
che Hérigone qualche tempo fa pubblicò nel suo Cours mathematique. Superai
tutte le asimmetrie con difficoltà, e alla fine del mio lavoro, d'improvviso,
ogni cosa divenne chiara ed ottenni un'equazione molto semplice che mi diede la
stessa proposizione del Sig. Descartes. Per un momento pensai di aver fatto un
errore perché non potevo immaginare di poter raggiungere le stesse conclusioni
per una via completamente differente.
Il
Sig. Descartes aveva assunto per una delle sue dimostrazioni che il moto della
luce incontra una resistenza maggiore nell'aria che nell'acqua, ed io ho
assunto esattamente l'opposto, come voi potete vedere nella copia della
dimostrazione che ho tentato di ripetere a memoria per darvi piena
soddisfazione, dato che l'originale è stato mandato al Sig. de la Chambre
seguendo la mia pigrizia solita. Ho ripetuto comunque i calcoli parecchie
volte, cambiando i dati di partenza, e son pervenuto sempre alle stesse
conclusioni. Questo ha confermato due cose: una è che l'opinione del Sig.
Descartes sulla legge di rifrazione è corretta e l'altra è che la sua
dimostrazione era sbagliata e piena di paralogismi.
I seguaci di Descartes hanno visto la mia dimostrazione che
fu data loro dal Sig. de la Chambre e dapprima furono inclini a rifiutarla,
nonostante che io educatamente ricordassi che avrebbero dovuto esser
soddisfatti che la vittoria apparteneva ancora al Sig. Descartes, dato che in
effetti la sua opinione era confermata per vera anche per mezzo di ragionamenti
differenti dai suoi, e che dopo tutto i più famosi conquistatori non si considerarono
meno fe]ici quando la vittoria era ottenuta per mezzo di truppe ausiliarie
invece che per mezzo delle loro proprie truppe. All'inizio non volevano sentir
ragioni, insistettero che la mia dimostrazione era falsa, perché non poteva
sussistere senza distruggere quella del Sig. Descartes che per loro era
superiore a qualunque altra.
Quando
i più capaci geometri che videro la mia dimostrazione sembrarono approvarla,
allora essi si congratularono con me per mezzo di una lettera del Sig.
Clairsellier, che è il gentiluomo che fu d'aiuto nella pubblicazione delle
lettere del Sig. Descartes. Essi definirono un miracolo che la stessa verità
fosse raggiunta al termine di due cammini completamente opposti e decisero di
lasciare l'intera questione irrisolta e di ammettere che essi non potevano
risolversi a preferire il Sig. Descartes o me stesso, e che i posteri avrebbero
giudicato.
E
siete voi, Signore, che siete destinato, per i vostri meriti eccezionali, ad
avere molto a che fare con la posterità ed a informarla, se lo credete giusto,
di questo famoso dibattito o, se preferite, di mettere questa umile lettera tra
le vostre carte inutili...