Huygens
L'ipotesi ondulatoria di Hooke e Pardies viene ripresa e sviluppata da C. Huygens (1629-95) nel Traité de la Lumière (1690). Punto di partenza del trattato è l'ottica cartesiana che Huygens vuole rifondare in termini ondulatori La luce, in questa concezione, non può essere, come affermava Cartesio, una tendenza al moto bensì moto ondulatorio reale. Se si accetta la prima ipotesi non e possibile, ad esempio, spiegare l'attraversamento di due fasci luminosi che si intersecano senza disturbarsi e, tanto meno, la loro propagazione nella stessa direzione in versi opposti, dal momento che non è pensabile che una stessa particella possa contemporaneamente tendere ai due moti. Se però si pensa ad un etere composto di particelle identiche dotate di grande elasticità e si suppone che il moto della luce abbia origine dagli urti tra queste particelle e quelle del corpo luminoso, due impulsi possono propagarsi così come un impulso meccanico si propaga in una fila di sfere identiche contigue perfettamente elastiche. Questa analogia meccanica giustifica anche l'ipotesi di una velocità della luce finita ma molto grande.
Nella definizione del modello Huygens si richiama anche all'analogia suono-luce, ma mentre il suono si propaga per rarefazioni e compressioni dell'aria, la luce si trasmette nello stesso modo in cui un impulso, nell'esempio già citato della fila di sferette, si comunica dalla prima sfera all'ultima lasciando le sfere intermedie in quiete; il moto della luce perciò deve avvenire senza trasporto di materia. Il suono richiede inoltre per propagarsi la presenza dell'aria come gli esperimenti di Torricelli e di Boyle, ai quali Huygens fa riferimento, avevano dimostrato; al contrario la luce, in un tubo di Torricelli in cui sia stato praticato il vuoto, continua a propagarsi e ciò deve implicare l'esistenza di un etere in grado di penetrare nella materia.
Il modo di propagarsi della luce nell'etere è spiegato da Huygens sulla base dell'ipotesi che ogni particella del corpo luminoso debba essere considerata come un centro di onde sferiche. Ma «poiché le percussioni al centro di queste onde non hanno successione regolare, non si deve supporre che un'onda ne segua un'altra ad uguale distanza» [1] Le onde luminose non hanno perciò carattere periodico ma piuttosto sono dovute a una produzione casuale di impulsi. Inoltre la produzione ondosa è regolata dal principio, noto ormai come «principio di Huygens», secondo il quale «ciascuna particella della materia in cui un'onda viaggia comunica il suo moto non solo alla particella vicina che è allineata con la sorgente luminosa, ma necessariamente anche alle altre con le quali è a contatto e che si oppongono al suo movimento. Cosicché intorno a ciascuna particella si origina un'onda di cui essa è il centro» [2]. Le onde secondarie sono efficaci solo quando concorrono a formare simultaneamente il fronte d'onda che è costituito perciò dall'inviluppo di tutti questi contributi elementari; con questa ipotesi additiva Huygens spiega la propagazione rettilinea della luce[3].
Sulla base del proprio principio Huygens dimostrerà le leggi della rifrazione, pervenendo alla formulazione corretta sen i/sen r = vi/vr, e le leggi della riflessione, ivi includendo la riflessione totale. L'autore estende poi il suo programma di ricerca al fenomeno della doppia rifrazione che sottopone a un'analisi quantitativa sperimentale assai accurata. Come è noto, quando la luce incide su un cristallo di spato di Islanda il raggio incidente si suddivide in due raggi, l'ordinario e lo straordinario, dei quali solo il primo segue la legge di rifrazione. Poichè nel mezzo in esame avvengono due rifrazioni, Huygens suppone che il raggio ordinario si propaghi nell'etere presente nel cristallo, dando luogo a onde elementari sferiche, mentre quello straordinario viene trasmesso sia dalle particelle del cristallo che da quelle dell'etere. Le onde secondarie, in questo caso, assumono una forma ellittica, o piuttosto sferoidale e si propagano nel mezzo con velocità diversa nelle diverse direzioni. Nel primo caso Huygens applica la costruzione per onde elementari già usata nella rifrazione ordinaria, nel secondo adatta lo stesso meccanismo ai fronti d'onda sferoidali.
Nel corso delle indagini lo scienziato osserverà ancora un fenomeno anomalo che non riuscirà a spiegare: se si dispongono a una certa distanza due cristalli di calcite A e B, in modo che le loro facce risultino parallele e si lascia incidere perpendicolarmente a esse un pennello luminoso, all'uscita da A si osserva la birifrangenza mentre all'uscita da B si verifica o meno una ulteriore suddivisione dei raggi a seconda dell'angolo di rotazione di B rispetto ad A [4]. Oggi sappiamo che un tale fenomeno e connesso con la polarizzazione della luce e che quindi non poteva in alcun modo essere interpretato con un'ipotesi di onde longitudinali. I tentativi di Huygens di spiegare il fenomeno saranno vani; lo stesso autore riconoscerà «di non essere in grado di individuarne le cause. Ma per questa ragione di non desistere dal descriverli con lo scopo di dare ad altri l'opportunità di indagarli» [5]
C.
Huygens, Traité de la lumière, pp. 41-48
Passiamo ora alla spiegazione degli effetti della
rifrazione supponendo, come abbiamo fatto, il passaggio delle onde luminose
attraverso i corpi trasparenti, e la diminuzione della velocità che esse vi
subiscono.
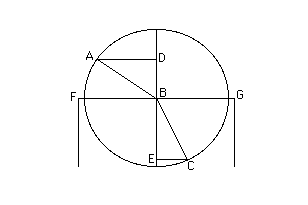
La principale proprietà della rifrazione consiste nel fatto
che quando un raggio di luce, come AB (cfr. fig. 1), proveniente dall'aria,
incide obliquamente sulla superficie liscia di un corpo trasparente come FG,
esso si interrompe nel punto di incidenza B, in modo da formare con la retta
perpendicolare alla superficie DBE un angolo CBE, minore di ABD. La misura di
questi angoli si trova tracciando un cerchio di centro B, che taglia i raggi
AB, BC. Le perpendicolari AD, CE condotte dai punti di intersezione sulla retta
DE, e chiamate seni degli angoli ABD, CBE, hanno tra loro un certo rapporto che
è sempre lo stesso per tutte le inclinazioni del raggio incidente ed è quindi caratteristico
di un certo corpo trasparente. Tale rapporto nel vetro si approssima come 3 a
2, nell'acqua come 4 a 3, e assume valori diversi in altri corpi diafani.
Un'altra proprietà simile a questa detta è che le
rifrazioni sono reciproche tra i raggi entranti in un corpo trasparente, e
quelli uscenti. E' come dire che se il raggio AB entrando nel corpo trasparente
si rifrange in BC, così CB, considerato come raggio all'interno dello stesso
corpo, si rifrangerà in BA uscendo.
Per spiegare dunque le ragioni di questi fenomeni seguendo
i nostri principi, sia AB la retta (cfr. fig. 2), che rappresenta una
superficie piana delimitante i corpi trasparenti che sono in direzione di C e
di N. Quando dico piana, non voglio intendere di una uguaglianza perfetta, ma simile
a quella che si intende trattando la riflessione.
La linea AC rappresenti una parte d'onda di luce, il cui
centro sia supposto così lontano, che questa parte possa essere considerata una
linea retta. Il punto C dell'onda AC in un certo intervallo di tempo sarà
avanzato fino al piano AB lungo la retta CB, che va considerata proveniente dal
centro luminoso e, per conseguenza, taglierà AC ad angolo retto. Ora, nello
stesso tempo, il punto A sarà arrivato in G per la retta AG, uguale e parallela
a CB e tutta la parte d'onda AC sarà in GB se la materia del corpo trasparente
trasmetteva il movimento dell'onda così velocemente come quello dell'etere.
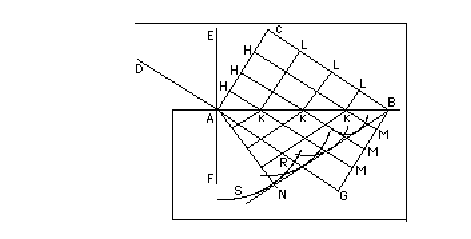
Supponiamo però che essa trasmetta questo movimento meno
velocemente, per esempio, di un terzo. Vi sarà una diffusione di movimento dopo
il punto A, nella materia del corpo trasparente, per una estensione uguale ai
due terzi di CB, che produce la sua onda sferica particolare, seguendo ciò che
è stato detto, onda che è dunque rappresentata dalla circonferenza SNR, con
centro in A, e il raggio uguale ai 2/3 di CB. Se consideriamo successivamente
le altre rette H dell'onda AC, nel medesimo tempo in cui il punto C è giunto in
B, esse non solo arriveranno alla superficie AB lungo le rette HK parallele a
CB, ma genereranno anche delle onde particolari nel diafano di centro K, qui
rappresentate da circonferenze i cui raggi sono uguali ai 2/3 di KM, cioè ai
2/3 dei prolungamenti di HK fino alla retta BG, poiché questi raggi sarebbero
stati uguali a KM, se i due diafani avessero avuto la stessa penetrabilità.
Ora tutte queste circonferenze hanno per tangente comune la
linea retta BN, che costituisce la stessa tangente dal punto B alla
circonferenza SNR che abbiamo considerata per prima. E' facile vedere che tutte
le altre circonferenze vanno a toccare la stessa BN, da B fino al punto di
contatto N. [...] E' BN dunque che può essere considerata come composta da
piccoli archi di queste circonferenze, che delimita il moto che l'onda C ha
comunicato nel corpo trasparente e ove questo movimento si trova in quantità
maggiore che altrove. Questa linea, seguendo ciò che è stato detto più di una
volta, è la propagazione dell'onda AC nel momento in cui il suo punto C è
arrivato in B. Poiché non vi è nessun'altra linea al di sotto del piano AB che,
al pari di BN, sia tangente comune di tutte le onde particolari in esame. Se si
vuole sapere come l'onda AC si è spostata in BN, non occorre far altro che
tracciare nella stessa figura tutte le rette KO parallele a BN, e tutte le
rette KL parallele ad AC: così si vedrà che l'onda CA, da piana si è rifratta
successivamente in tutte le spezzate LKO, di nuovo piane in BN e che ciò è
talmente evidente, per quanto è stato indicato, che non vi è bisogno di
chiarirlo ulteriormente.
Ora nella stessa
figura si conduca EAF, che interseca il piano AB ad angoli retti nel punto A e
AD sia perpendicolare all'onda AC; allora DA indicherà il raggio di luce
incidente e AN, perpendicolare a BN, il raggio rifratto dato che i raggi non
sono altro che linee rette lungo le quali i fronti d'onda si estendono. E'
facile riconoscere questa principale proprietà delle rifrazioni: che il seno
dell'angolo DAE ha sempre uno stesso rapporto con il seno dell'angolo NAF,
qualunque sia l'inclinazione del raggio DA, e che questo rapporto è lo stesso
di quello della velocità delle onde nel diafano dalla parte di AE, rispetto
alla loro velocità nel diafano dal lato AF. Considerando AB come raggio di un
cerchio, il seno dell'angolo BAC è BC, e il seno di ABN è AN. Ma l'angolo BAC è
uguale a DAE, poiché ciascuno di essi, aggiunto a CAE, fa un angolo retto. E
l'angolo ABN è uguale a NAF, dato che ciascuno di essi aggiunto a BAN fa un
angolo retto. Dunque il seno dell'angolo DAE sta al seno di NAF come BC ad AN.
Ma il rapporto di BC ad AN era uguale a quello delle velocità della luce nel
mezzo dalla parte di AE con quello della parte di AF: dunque, ancora, il seno
dell'angolo DAF starà al seno dell'angolo NAE come il rapporto delle velocità
della luce nei due mezzi. Per esaminare in seguito il comportamento della
rifrazione nel caso in cui le onde luminose passano in un corpo, in cui il moto
si propaga più velocemente rispetto al mezzo da cui esse provengono (supponiamo
che ciò avvenga di nuovo secondo un rapporto di tre a due) non dobbiamo far
altro che ripetere la stessa costruzione e dimostrazione, limitandoci a
sostituire, in luogo di 2/3, dappertutto 3/2. E si troverà con lo stesso
ragionamento, in quest'altra figura (cfr. fig. 3), che quando il punto C
dell'onda AC sarà pervenuto alla superficie AB nel punto B, tutta la parte
d'onda AC sarà avanzata fino a BN, in modo tale che BC, perpendicolare ad AC,
stia ad AN, perpendicolare a BN come 2 sta a 3. E questo medesimo rapporto di 2
a 3 starà come il seno dell'angolo EAD sta al seno dell'angolo FAN.
Da qui si vede la reciprocità delle rifrazioni di un raggio
che entra ed esce da uno stesso mezzo: ciò equivale a dire che se NA incide
sulla superficie esterna AB e si rifrange in AD, DA uscendo dal mezzo si
rifrangerà in AN.
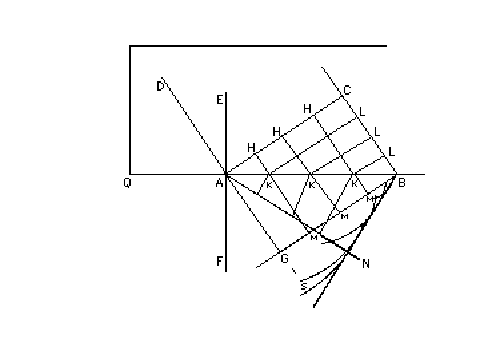
Si vede così il motivo di un fatto notevole che interviene
in questa rifrazione: dopo una determinata inclinazione del raggio incidente
DA, quest'ultimo incomincia a non poter penetrare nell'altro mezzo. Se l'angolo
DAQ o CBA è tale che nel triangolo ACB, CB sia maggiore o uguale ai 2/3 di AB,
allora AN non può essere lato del triangolo ANB, perché diviene uguale o
maggiore di AB: in questo modo non si forma alcuna parte dell'onda BN, né per
conseguenza AN, che deve essere la sua perpendicolare. E così il raggio incidente
DA non supera la superficie AB.
Quando il rapporto delle velocità delle onde, come nel nostro esempio, è di 2 a 3, che corrisponde al vetro e all'aria, l'angolo DAQ deve essere più grande di 48°11' affinché il raggio DA possa rifrangersi. E quando il rapporto di velocità è di 3 a 4, come è pressappoco nell'acqua e nell'aria, l'angolo DAQ deve superare 41° 24'. E ciò si accorda perfettamente con l'esperienza.