Tolomeo
Il grande astronomo Claudio Tolomeo appartiene alla scuola di Euclide alla quale reca specifici contributi di ricerca, sia sperimentale che teorica. Egli, sostituendo come base della prospettiva una piramide al cono, sostiene che l'occhio avverte la direzione e la lunghezza dei raggi emessi e studia la questione del giudizio sulla grandezza degli oggetti osservati, combinando la lunghezza della piramide prospettica con la grandezza della sua base. Di particolare rilievo sono i risultati sperimentali sul rapporto tra gli angoli di incidenza e quelli di rifrazione, una delle prime tappe verso la definizione della legge della rifrazione.
Con uno strumento costituito da un cerchio graduato munito al centro di due indici per facilitare la misurazione degli angoli di incidenza i e di rifrazione r, Tolomeo ricava una serie di misure nei mezzi aria-acqua, aria-vetro, acquavetro. Nel caso del passaggio della luce da un mezzo più denso a uno meno denso stabilisce il valore dell'angolo limite per l'acqua. Per gli angoli di incidenza e di rifrazione egli individua una relazione che associa a un valore dato di i, il rapporto i/r. Questa assunzione verrà da molti intesa come una legge del tipo i/r = costante, risultato questo che, per piccoli valori di i, e in buon accordo con la legge della rifrazione.
Ma più esattamente la relazione che Tolomeo stabilisce tra i e r è di tipo parabolico: ciò si può desumere dalla costanza delle differenze seconde riportate nelle sue tabelle.
Si può supporre che una volta riscontrata la coincidenza dei primi risultati sperimentali con i punti di una parabola Tolomeo abbia ricavato geometricamente i successivi valori senza realmente eseguire le misure. In ogni modo, rispetto alla relazione lineare tra angoli di incidenza e di rifrazione, largamente usata nel seguito anche da Keplero, la relazione parabolica di Tolomeo approssima meglio la legge di rifrazione .
L'ipotesi emissionista sostenuta da Tolomeo fa sì
che nella lettura dei brani le definizioni di angoli dí incidenza e rifrazione
siano invertite rispetto all'uso corrente. Da rilevare anche il brano finale in
cui Tolomeo allude a un'interpretazione unitaria della legge di riflessione e
di rifrazione tramite un principio metodologico più generale, il «principio di
minimo». Purtroppo lo sviluppo di questa argomentazione, risalente
originariamente ad Aristotele, è andato perso.
L'Ottica di Claudio Tolomeo cit., libro V, pp. 144-50
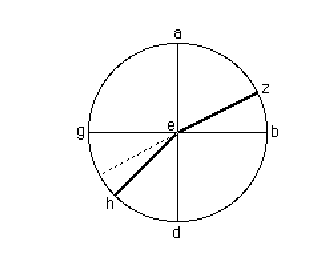 La misura della flessione che avviene in acqua e che può
essere osservata, è determinabile con un esperimento (cfr. fig. 1) simile a
quello che abbiamo condotto con l'aiuto del disco di rame, per studiare le
leggi degli specchi: su di esso si descriva un cerchio ABGD con centro in E e i
due diametri AEG e BED che si intersecano ad angoli retti; si divida ogni
quadrante in 90 parti uguali e si ponga nel centro un piccolo indice colorato.
Posto il disco in posizione verticale in un piccolo recipiente, si versi in
esso acqua limpida in quantità moderata e penetrabile allo sguardo Facciamo si che la superficie del disco sia
perpendicolare alla superficie dell'acqua e che metà del cerchio, cioè BGD, si
trovi interamente sotto l'acqua con il diametro AEG perpendicolare alla
superficie dell'acqua.
La misura della flessione che avviene in acqua e che può
essere osservata, è determinabile con un esperimento (cfr. fig. 1) simile a
quello che abbiamo condotto con l'aiuto del disco di rame, per studiare le
leggi degli specchi: su di esso si descriva un cerchio ABGD con centro in E e i
due diametri AEG e BED che si intersecano ad angoli retti; si divida ogni
quadrante in 90 parti uguali e si ponga nel centro un piccolo indice colorato.
Posto il disco in posizione verticale in un piccolo recipiente, si versi in
esso acqua limpida in quantità moderata e penetrabile allo sguardo Facciamo si che la superficie del disco sia
perpendicolare alla superficie dell'acqua e che metà del cerchio, cioè BGD, si
trovi interamente sotto l'acqua con il diametro AEG perpendicolare alla
superficie dell'acqua.
Ora si prenda un arco AZ [misurato a partire] dal punto A
in uno dei due quadranti del disco che si trovano al di sopra dell'acqua e si
ponga anche su Z un piccolo indice colorato. Guardiamo con un occhio fino a che
idue indici in Z e in E compaiono allineati sul raggio che procede dall'occhio
e spostiamo una sottile assicella lungo l'arco che si trova sul quadrante
opposto immerso in acqua, cioè GD, fino a che l'estremità dell'assicella appaia
dalla parte opposta rispetto ai due indici. Ora, se misuriamo l'arco tra il
punto G e il punto [H], rispetto al quale [l'assicella] appare in linea retta,
troveremo che questo arco GH sarà sempre minore all'arco AZ e se congiungiamo
ZE ed EH, l'angolo AEZ sarà maggiore dell'angolo GEH; ma questo accade solo se
c'è deviazione, cioè se il raggio ZE devia verso H, a seconda della quantità in
base a cui uno dei due angoli opposti differisce dall'altro. Se ora poniamo
l'occhio sopra la perpendicolare AE, il raggio visuale non sarà deviato ma
cadrà in G opposto [ad A] e sulla linearetta [AE].
In tutte le altre posizioni tuttavia al crescere dell'arco
AZ, GH crescerà e sarà anche maggiore la deviazione del raggio [rispetto al
prolungamento del raggio incidente] (cfr. tab. 1).
Tabella 1.
Misura dell'arco Misura dell'arco
AZ in gradi
GH in gradi
angoli di
incidenza angoli di incidenza
X VIII
XX XV e mezzo
XXX XXII e mezzo
XL XXIX
L XXXV
LX XL e mezzo
LXX XLV e mezzo
LXXX L
Così abbiamo scoperto le quantità di deviazione che
avvengono in acqua ma non abbiamo trovato una differenza sensibile con acqua di
diversa densità.
Ora se noi conduciamo osservazioni dall'acqua di densità
naturale ad un mezzo più rarefatto, ci sarà una differenza considerevole
nell'aumento degli angoli e della quantità di flessione nel passaggio del
raggio dall'acqua più densa, a quella più rarefatta.
Ma poiché per noi è impossibile osservare in un esperimento
come quello che abbiamo appena descritto, il comportamento della deviazione che
si ha quando il raggio procede da un liquido più denso ad uno più rarefatto,
abbiamo adottato il metodo seguente per misurare gli angoli.
Si abbia un semicilindro di vetro puro, simile a metà del
disco, definito dall'arco TKL; il suo diametro sia minore di quello del disco
di rame sopramenzionato (cfr. fig. 2). Adattiamo la sua base al disco in modo
che risulti tutta in contatto con esso, e il centro comune sia in E. Il
diametro TL giaccia sul diametro BD e AE sia perpendicolare alla parte piana
della superficie di vetro. Pertanto, tutte le linee tracciate da E agli archi
BGD e TKL saranno perpendicolari.
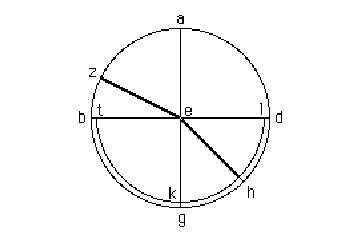
Ora, se conduciamo questo esperimento come abbiamo fatto
per quello precedente, poniamo un piccolo indice sulla superficie appena su E,
punto medio del lato del semicilindro, e guardiamo con un occhio lungo la linea
AE verso il bordo del vetro; [cosl facendo], spostiamo un oggetto lungo l'arco
opposto a quello da cui stiamo osservando fino a che esso ci apparirà davanti.
L'oggetto si troverà sopra il punto G, perché la linea AEG è perpendicolare sia
a TEL che a TKL.
E se cambiamo il nostro punto di vista in una posizione
[diametralmente opposta ad A] e guardiamo nella direzione di GE, un oggetto
spostato sulla circonferenza opposta del disco sarà visto opposto a GE, in
direzione di EA. Per la stessa ragione di prima non ci sarà deviazione
all'uscita dal vetro all'aria.
Ora, preso un arco misurato da A, AZ, e tracciata la linea
ZE, colorata di nero, guardiamo lungo di essa fino a che un oggetto mosso
dietro il vetro è visto in direzione della stessa linea. Se segnamo con un
altro indice quel punto H che abbiamo trovato quando il colore nero [la linea
ZE] appariva continuo con EH, troveremo anche, in questo caso, che l'angolo AEZ
è maggiore dell'angolo GEH e per di più troveremo che l'eccesso di un angolo
sull'altro è maggiore che nel caso dell'acqua, a parità di distanza [per uno
stesso angolo di incidenza].
E ancora, quando l'occhio è sul punto H, che è opposto al
punto E e guardiamo da H in direzione di HE, entrambi i punti [E e Z]
appariranno sulla stessa identica linea. Ma poiché il raggio subiva una deviazione
nel punto [E], ne segue che, sia che esso procedesse dall'aria al vetro, come
faceva ZE, venendo deviato lungo EH, sia che procedesse dal vetro all'aria
venendo deviato lungo EZ, in entrambi i casi si aveva una deviazione in
direzione di T. E poiché le perpendicolari che sono tirate da E all'arco TKL
sono tutte simili, esse non sono deviate sia che [i raggi che esse
rappresentano] sono considerati entranti o uscenti da E.
Ora se in questo caso ancora, desideriamo trovare la
quantità di deviazione in ogni posizione, poniamo l'occhio successivamente in
ciascuna delle posizioni assunte nell'esperimento precedente, variando l'angolo
formato rispetto ad E (che contiene la perpendicolare e il raggio EZ). I
risultati sono i seguenti [... (cfr. tab. 2).
Tabella 2.
Misura dell'arco Misura dell'arco
AZ in gradi GH in gradi
angoli di
incidenza angoli di rifrazione
X
VII
XX XIII e mezzo
XXX
XIX e mezzo
XL
XXV
L
XXX
LX XXXIV e mezzo
LXX
XXXVIII e mezzo
LXXX XLII
Ma si trova che la quantità di deviazione sarà minore
quando il vetro è posto in prossimità dell'acqua poiché la differenza delle
deviazioni [la differenza tra gli angoli di incidenza e di rifrazione], nel
passaggio di un raggio visuale da uno di questi corpi all'altro non è grande;
infatti la differenza di densità tra acqua e vetro è minore di quella tra
l'aria e l'acqua o tra l'aria e il vetro. Ma noi siamo in grado anche in questo
caso di determinare la quantità di deviazione, come ora spiegheremo: adattiamo
un semicilindro di vetro al disco di rame e sistemiamolo in modo tale che
conservi la posizione in cui il centro [del bordo piano] coincida con quello
del disco (cfr. fig. 3). Coloriamo di nuovo il punto E e poniamo verticalmente
il disco di rame in un recipiente, ad angoli retti rispetto alla superficie
dell'acqua e per metà sotto l'acqua, trovandosi la parte ricurva del vetro,
TKL, nella zona superiore. Versiamo nel recipiente una quantità d'acqua in modo
che il bordo TEL si trovi appena sopra la superficie dell'acqua.
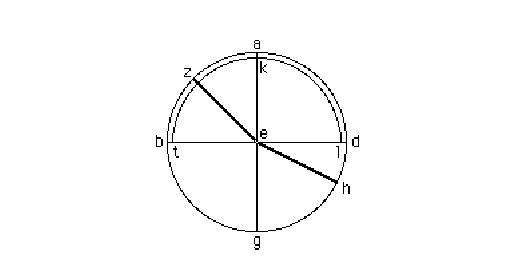
Ora si prenda l'arco GH nel mezzo meno denso, cioè
nell'acqua, contenente, diciamo, 10°. Segnamo H con un piccolo indice colorato
e guardiamolo con un occhio finché un oggetto Z, che si stia muovendo sull'arco
AB, sia visto lungo la direzione del punto H e del punto colorato E. Fatto ciò,
tiriamo le due linee EH ed EZ. Se allora desideriamo misurare sull'arco AB
l'angolo che si trova nel mezzo più denso, cioè nel vetro, quando l'angolo
nell'acqua, misurato dalla perpendicolare, cioè l'angolo GEH varia, troveremo i
risultati seguenti [ . . . ] (cfr. tab. 3).
Tabella 3
Misura dell'arco Misura dell'arco
GH in gradi AZ in gradi
angoli di
incidenza angoli di rifrazione
X XIX e mezzo
XX XXIII e mezzo
XXX XXVII
XL XXXV
L XLII e mezzo
LX XLIX e mezzo
LXX LVI
LXXX LXII