Cartesio
Nel 1637 Cartesio pubblica, insieme ad altri due trattati, le Météores e la Géométrie, uno studio organico sull'ottica, la Dioptrique. Nella prefazione, dal titolo Discours de la méthode, Cartesio, tra l'altro, definisce alcune regole metodologiche «per ben condurre la propria ragione e cercare la verità nelle scienze».
La fisica cartesiana poggia su due livelli di spiegazione, il primo dei quali e connesso ad alcune verita a priori che costituiscono un vero e proprio sistema di assiomi (la materia è pura estensione, e infinitamente divisibile, il vuoto non esiste, tutti i moti sono circolari, la quantità di moto dell'universo è costante, ecc.); il secondo livello è costituito da un sistema ipotetico-deduttivo che comunque non deve essere in contraddizione con le verità a priori. Il ricercatore può fare appello all'esperimento la cui funzione tuttavia si deve limitare a confermare, piuttosto che a provare, certe conclusioni compatibili con le verita a priori.
Le concezioni sulla natura della luce vengono fatte discendere da Cartesio dal primo livello, come conseguenza del principio metafisico in base al quale il movimento è l'unico potere esistente in natura.
L'ipotesi che sta alla base della Dioptrique è appunto che la luce sia un'azione o un movimento che obbedisce alle stesse leggi del moto locale e che si trasmetta in un tutto pieno. Essa però non corrisponde a un moto effettivo ma piuttosto a una tendenza al movimento, a una pressione che si propaga istantaneamente dalla sorgente luminosa agli occhi dell'osservatore.
Per Cartesio, il plenum di materia, in conseguenza del moto primario impresso da Dio, si era suddiviso in tre categorie di particelle, diverse per forma, dimensioni e velocità. Le particelle più piccole e leggere non hanno forma, e di esse sono costituite le stelle e il sole, quelle più grandi, dotate di minore velocità, hanno forma sferica e riempiono gli spazi interplanetari, le ultime, e le più lente, costituiscono la materia della terra e dei pianeti. La luce per Cartesio è generata proprio dalle pressioni che la prima classe di particelle esercita su quelle della seconda e i raggi luminosi sono le linee lungo le quali queste pressioni (o tendenze al moto) si manifestano.
La concezione sulla luce viene così ulteriormente chiarita da Cartesio: «Voglio che voi pensiate che la luce, nei corpi che chiamiamo luminosi, non è altro che un certo movimento o azione molto rapida e violenta che giunge ai nostri occhi attraverso la mediazione di un bastone. Questo vi eviterà fin dall'inizio di trovare strano che la luce possa estendere i suoi raggi in un istante dal sole a noi: giacché voi sapete che l'azione con cui viene mossa l'estremità del bastone passa all'altra in un istante» [1].
Incapace di una deduzione rigorosa, per dare un'interpretazione della legge della riflessione Cartesio fa uso di una analogia meccanica con il caso di un proiettile che rimbalza su una superficie elastica (nella storia dell'ottica questa analogia è di vecchia data: di essa già si erano serviti Tolomeo, Alhazen, Bacone e Keplero). Egli suppone cioè che la luce, o moto in potenza, poiché obbedisce alle stesse leggi del moto locale, possa venir considerata come moto in atto e quindi messa in corrispondenza con il comportamento mec- canico del proiettile. Poiché la superficie riflettente non ha alcuna influenza sul suo moto, la velocità di incidenza del proiettile deve essere uguale a quella di riflessione: Vi = Vr. La componente orizzontale del moto, inoltre, si deve conservare cosicché: Vi sen i = Vr sen r, da cui segue l'uguaglianza tra l'angolo di incidenza e quello di riflessione (l'interpretazione della legge della riflessione viene qui data ovviamente in linguaggio moderno. Cartesio in realtà non parla mai di velocità ma piuttosto di una «determinazione della luce al movimento»).
Anche per la rifrazione Cartesio si basa sull'analogia meccanica: la luce, quando passa da un mezzo meno denso a uno più denso, si comporta, in sostanza, come una palla da tennis che penetra ad esempio dall'aria in acqua. La conclusione però è diversa nei due casi, mentre la luce, nel passaggio aria-acqua si avvicina alla normale alla superficie, la palla se ne allontana. «Questo fatto, — afferma Cartesio, — non risulta più strano se vi richiamerete alla natura che ho attribuito alla luce quando affermavo che essa altro non è che una specie di movimento o di azione concepita in una materia sottilissima che riempie i pori di tutti i corpi». Così Cartesio spiega che mentre una palla rallenta maggiormente il suo moto quando colpisce un corpo cede- vole, la luce viene << trattenuta di più dalle particelle di aria [...] che da quelle di vetro. Avviene così, che quanto più le particelle di un corpo sono dure e stabili, tanto più facilmente fanno passare la luce» [2].S
Per arrivare a stabilire la legge della rifrazione Cartesio parte da due assunzioni: le velocità di rifrazione e d'incidenza stanno tra loro nella relazione vr = nvi, dove n è una costante caratteristica dei mezzi. La componente parallela della velocità, inoltre, deve conservarsi di modo che vi sen i = vr sen r. Dalle due assunzioni segue la legge sen i/sen r = vr/vi = n.
Sulla priorità
della scoperta della legge di rifrazione, che Cartesio attribuisce a se stesso,
le opinioni sono discordi. Tuttavia è certo che già Thomas Harriot (1560 ca.-
1621) ne avesse individuato la legge in termini geometrici come rapporto di
segmenti corrispondenti agli indici di rifrazione, ma non ne aveva pubblicato i
risultati. Nello stesso periodo la legge veniva pubblicata da W. Snell (1591-
1626) sotto forma di un rapporto di cosecanti. Secondo alcuni Cartesio si
sarebbe anzi limitato a modificare la legge di Snell costruendone poi, a
posteriori, la dimostrazione. Del resto, la spiegazione fisica che Cartesio da
del fenomeno, condotta in un linguaggio spesso assai oscuro e controverso,
lascia insorgere non poche perplessita.
Cartesio, Dioptrique , in OEuvres
de Descartes , II, VI, pp. 98-100
Veniamo adesso alla rifrazione. Dapprima supponiamo che una
palla lanciata da A verso B (cfr. fig.) incontri nel punto B non più la
superficie della terra, ma un corpo CBE, che sia così tenue e sottile che la
palla può romperlo e passarci interamente attraverso, perdendo solo una parte
della sua velocità, ad esempio una metà di questa. Ora, avendo assunto ciò, al
fine di determinare quale cammino dovrebbe seguire, notiamo dapprima che il suo
moto differisce interamente dalla sua tendenza a muoversi in una direzione
piuttosto che in un'altra, dal che segue che le quantità di questi moti
dovrebbero essere considerate separatamente. E notiamo anche che delle due
parti di cui possiamo immaginare che questa tendenza sia composta, solo quella
parte che farebbe muovere la palla dall'alto in basso può essere modificata in
qualsiasi modo dall'impatto sul tessuto, mentre la tendenza che la fece muovere
verso destra dovrebbe rimanere sempre la stessa di prima, perché il tessuto non
è affatto opposto ad essa in questo senso [...].
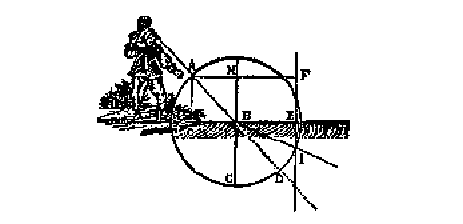
Supponiamo adesso che la palla, muoventesi da A verso D,
incontri nel punto B non più un corpo ma dell'acqua, la cui superficie CBE la
privi di metà della sua velocità, così come accadeva per il tessuto. [...]
Facciamo adesso un'altra ipotesi e assumiamo che la palla,
che all'inizio si muoveva da A a B, sia spinta proprio quando è nel punto B
dalla racchetta CBE che aumenta la forza del moto, per esempio, di un terzo,
cosicché essa continua a muoversi in due istanti su una distanza grande quanto
[quella sulla quale essa] prima si muoveva in tre istanti. Ciò avrà lo stesso
effetto che se la palla avesse incontrato nel punto B un corpo di tal natura da
farla passare attraverso la superficie CBE con una facilità 1/3 maggiore che
attraverso l'aria. [...]
Per concludere, nella misura in cui l'azione della luce
segue in questo aspetto le stesse leggi del moto della palla, dobbiamo dire che
quando i suoi raggi passano obliquamente da un corpo trasparente ad un altro,
che li riceve più o meno facilmente del primo, essi ruotano in modo da essere
sempre meno inclinati verso la superficie di separazione di questi mezzi dalla
parte in cui c'è il corpo che li riceve più facilmente, che dall'altra, e ciò
proprio nella proporzione in cui sta quello che li riceve più facilmente
rispetto all'altro. [...]
Ma forse resterete stupiti, nel fare questi esperimenti, di
trovare che i raggi di luce sono più inclinati rispetto alla superficie di
rifrazione in aria che in acqua; e ancora più in acqua che in vetro,
esattamente all'opposto del comportamento di una palla, che è più inclinata
rispetto alla superficie in acqua che in aria e non può entrare affatto nel
vetro. Per esempio se una palla, che è spinta in aria da A a B (cfr. fig.),
incontra la superficie dell'acqua CBE nel punto B, sarà deflessa da B verso V;
se si tratta invece di un raggio di luce andrà al contrario da B verso I.
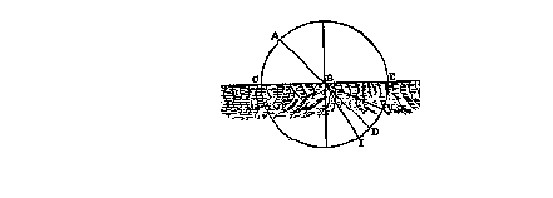
Smetterete, comunque, di trovarlo un effetto strano,
ricordando la natura da me attribuita alla luce, quando dissi che non è altro
che un certo moto o un'azione concepita in una materia molto sottile, che
riempie i pori di tutti gli altri corpi e considerando che, come una palla,
perde più del suo moto quando urta contro un corpo morbido che contro uno duro,
e che essa rotola meno facilmente su un tavolo ricoperto di tessuto che su uno
levigato; così l'azione di questa materia sottile può essere frenata molto più
dalle parti d'aria che, essendo come sono soffici e debolmente legate una
all'altra, non offrono molta resistenza ad essa, che dalle parti dell'acqua,
che offrono più resistenza e ancor più dalle parti d'acqua che da quelle del
vetro o cristallo.
Pertanto avviene che, quanto più le particelle di un corpo trasparente sono rigide e stabili, tanto più permettono alla luce di passare facilmente; perché la luce non dovrebbe spingerne nessuna fuori posto, come una palla deve invece spingere via le parti dell'acqua per trovare un passaggio tra di esse.