Fig. 13
scheda 1 - descrizione dell'esperimento di michelson e morley nell'ipotesi dell'etere immobile (senza l'ipotesi di contrazione di lorentz)
sistema di riferimento solidale con l'etere [65]
BRACCIO ORIZZONTALE
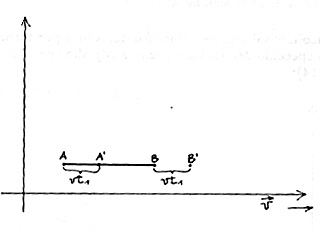
- Calcoliamo il tempo impiegato dalla luce per andare dallo specchio M allo specchio M l (Fig.13):

Fig. 13
Lo specchio M si trova inizialmente nella posizione A dell'etere, lo specchio M l nella posizione B dell'etere.
La distanza percorsa dalla luce per andare dallo specchio M allo specchio M l è (l + vt 1 ), perchè lo specchio M l fugge davanti al raggio di luce che lo raggiunge quando esso si trova nel punto B' dell'etere; t l è il tempo effettivo che la luce impiega in questo sistema per andare da A a B' e perciò t l è anche il tempo che lo specchio M l impiega per andare da B a B'.
Quindi
da cui
Nel tempo t l lo specchio M si è spostato dalla posizione iniziale A nella posizione A'.
- Calcoliamo il tempo impiegato dalla luce per tornare dallo specchio M l (nella posizione B') allo specchio M (Fig . 14):
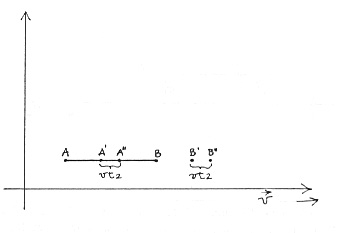
Fig.14
Lo specchio M si muove incontro al raggio di luce con velocità [[upsilon]], spostandosi dalla posizione A' alla posizione A" nel tempo t 2, che è lo stesso tempo impiegato dalla luce per andare dal punto B' (dove si era spostato M l ) al punto A" (dove si trova infine M). La distanza percorsa dalla luce è quindi: (l + vt 2).
Perciò
da cui
Il tempo totale impiegato dalla luce per andare dallo specchio M allo specchio M l e tornare è:
BRACCIO VERTICALE
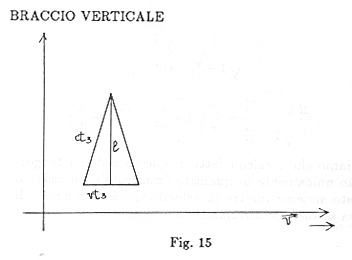
Mentre la luce viaggia dallo specchio M a M 2, la Terra si sposta rispetto all'etere di un piccolo tratto nella direzione del suo moto e quindi lo specchio M 2, va a trovarsi nel punto A dell'etere secondo la Fig.15. B è la posizione occupata nell'etere dalla lastra M quando la luce arriva allo specchio M 2, nella posizione A; C è la posizione nell'etere della lastra M quando la luce arriva di ritorno su di essa. Indicando con t 3 il tempo impiegato dalla luce per percorrere la distanza MA, calcoliamo con il teorema di Pitagora
da cui
E il tempo totale, sempre con la approssimazione di prima è
Notiamo che i calcoli fatti in questo sistema tengono conto unicamente di quantità "misurabili" in esso. In questo sistema inoltre la velocità della luce non è diversa secondo le direzioni, ma è sempre c.
Sistema di riferimento solidale con la Terra[66]
BRACCIO ORIZZONTALE
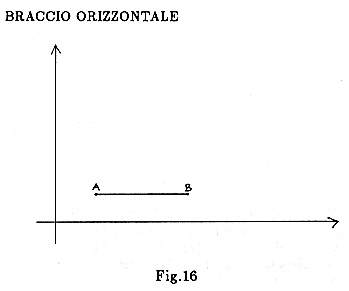
Gli specchi sono fermi mentre la luce si muove in questa direzione con velocità (c - v) e (c + v) secondo il verso (vedi Fig.16). Si ricava (vedere i calcoli nel cap. 3) che il tempo totale è
Dal punto di vista classico il tempo totale deve essere lo stesso nei due sistemi.
BRACCIO VERTICALE
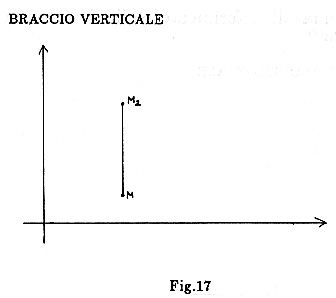
Nel sistema solidale con la Terra l'osservatore vede la luce che va su e giù tra gli specchi M ed M 2 (fissi), con Velocità diversa da c (vedi Fig.17). La velocità della luce è c rispetto all'etere, nel cui sistema però la luce compie un cammino diverso (Fig.18):
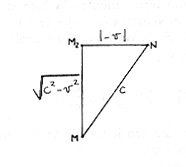
Fig.18
Sull'ipotenusa è la velocità della luce nell'etere, sul cateto M 2N la velocità dell'etere rispetto alla Terra, sul cateto MM 2 la velocità della luce rispetto alla Terra. Le velocità si compongono secondo la composizione classica. Essendo, rispetto alla Terra, la distanza totale percorsa dalla luce su questo braccio uguale a 2l e la velocità uguale a , il tempo totale di percorrenza è:
che è uguale a 2t 3 .
Notiamo esplicitamente che, per trovare la velocità della luce in questo sistema, Lorentz, avendo a disposizione il risultato che la velocità della luce rispetto all'etere è c, applica la composizione classica delle velocità, il che equivale ad accettare le trasformazioni galileiane. L'uguaglianza dei tempi calcolati in questo caso nei due sistemi segue quindi naturalmente dall'aver basato l'impostazione del calcolo su questa assunzione.
Nelle relazioni matematiche calcolate per i tempi nei due sistemi compaiono al denominatore le espressioni (c + v) e (c - v). Nel secondo sistema, solidale con la Terra, (c + v) e (c - v) sono le velocità della luce nei due versi. Nel primo sistema, solidale con l'etere, non c'è alcun ente fisico che si muove con velocità (c - v) e (c + v) rispetto all'etere. Infatti la luce ha velocità c e gli specchi velocità v.
Scheda 2 - Descrizione dell'esperimento di Michelson e Morley secondo la Relatività Speciale di Einstein
Sistema di riferimento proprio
(cioè solidale con l'apparato, quindi con la Terra)
Ricordiamo soltanto che per ogni braccio la distanza percorsa è 2l, la velocità della luce è c, il tempo totale di percorrenza è
Sistema di riferimento "dell'etere di Lorentz"
(cioè un sistema inerziale che si muove con velocità -v rispetto all'apparato)
BRACCIO ORIZZONTALE
- Partiamo da quanto asserito dalla Relatività Speciale riguardo alla misura di un regolo di lunghezza propria l, fatta da un osservatore inerziale che si muove con velocità v (Fig.l9):
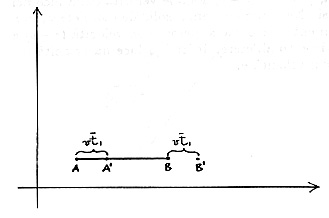
Fig.19
Questo osservatore misura per la lunghezza del braccio orizzontale
Per questo osservatore la luce va dal primo al secondo specchio (M Ml), cioè dal punto A al punto B' mentre lo specchio M l compie il percorso BB', nello stesso tempo t l. Perciò la luce percorre il tratto
da cui
- Analogamente, nel ritorno la luce va da B' ad A" nello stesso tempo t2 in cui lo specchio M si è spostato da A' ad A" e lo specchio M l da B' a B" (Fig.20):
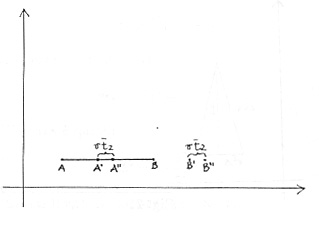
Fig. 20
Perciò è
da cui
Il tempo totale è
BRACCIO VERTICALE
(Vedere i calcoli nella Scheda 1 - Braccio verticale). Risulta (vedi Fig.21):
Notiamo che per entrambi i bracci i tempi di percorrenza della luce sono uguali e quindi anche in questo sistema di riferimento non si prevede spostamento della figura di interferenza: i due sistemi sono equivalenti.
Inoltre notiamo che:
dove t è il tempo proprio, secondo la trasformazione relativistica del tempo.
Scheda 3 - Calcoli ricostruiti da Lorentz (1892) [67]
Il tempo richiesto dalla luce per viaggiare su e giù fra due punti rigidamente fissati alla Terra la cui distanza è l, parallelamente alla direzione del moto, è
Mentre perperndicolarmente
La differenza è quindi
L'accorciamento sufficiente per compensare t sia [[Delta]]l = l[[alpha]] dove [[alpha]] è da calcolare. Quindi la lunghezza del braccio parallelo sia
l - l[[alpha]] = l (1 - [[alpha]] )
Per calcolare ([[alpha]], introduciamo questa espressione in quella dei tempi:
Nel 1892, senza ulteriori spiegazioni, Lorentz suppone che si possa trascurare il termine
Per rendere quindi t l + t 2= 2t 3 , rimane da porre
da cui
Scheda 4- Le ipotesi del 1895 [68]
Nel 1895 Lorentz avanza una ipotesi analoga a quella della contrazione, anche se più complessa. Ci sarebbe la stessa differenza fra i tempi di percorrenza della luce lungo il braccio perpendicolare e quello parallelo, se il braccio parallelo rimanesse lungo l e quello perpendicolare si allungasse della quantità . Oppure, più in generale, si potrebbe immaginare che "il moto di un corpo solido attraverso l'etere a riposo eserciti sulle dimensioni di questo corpo una influenza che varia secondo l'orientazione del corpo rispetto alla direzione del moto". Se, per esempio, le dimensioni parallele a questa direzione fossero cambiate nel rapporto
e quelle perpendicolari nel rapporto,
allora dovremmo avere l'equazione
Infatti, nel 1892 Lorentz calcolava "la differenza fra il braccio perpendicolare e quello parallelo" (nell'ipotesi di contrazione di quello parallelo)
Adesso le lunghezze sono:
per il braccio parallelo l (1 + d ),
per il braccio perpendicolare l (1 + [[epsilon]] ).
Perciò
Quindi deve essere
In seguito, nella stessa parte del trattato del 1895, Lorentz decide, per coerenza con il resto della propria teoria, di assumere l'ipotesi della sola contrazione del braccio parallelo.
Questo porta ai valori